Given:
Mass attached to the left-hand side = 3 kg
Mass attached to the right-hand side = 5 kg
Let's find the magnitude of the instantaneous acceleration of the system when it is released from rest.
Apply the formula:
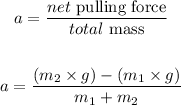
Where:
m1 = 3 kg
m2 = 5 kg
g = 9.8 m/s^2
Thus, we have:
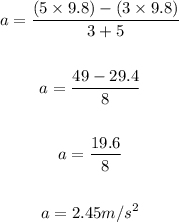
The magnitude of the instantaneous acceleration is 2.45 m/s².
ANSWER:
2.45 m/s²