Question

A rope is run over a massless pulley. The left-hand side of the rope is attached to a 3 kg mass, which rests on the ground. The right side of the rope is attached to a 5 kg mass, which is some unknown height above the ground. The system is released from rest. What is the magnitude of the instantaneous acceleration of the system when it is released from rest?

Answer 1

Given:

Mass attached to the left-hand side = 3 kg

Mass attached to the right-hand side = 5 kg

Let's find the magnitude of the instantaneous acceleration of the system when it is released from rest.

Apply the formula:

`\begin{gathered} a=\frac{net\text{ pulling force}}{total\text{ mass}} \\ \\ a=((m_2* g)-(m_1* g))/(m_1+m_2) \end{gathered}`

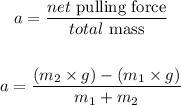
Where:

m1 = 3 kg

m2 = 5 kg

g = 9.8 m/s^2

Thus, we have:

`\begin{gathered} a=((5*9.8)-(3*9.8))/(3+5) \\ \\ a=(49-29.4)/(8) \\ \\ a=(19.6)/(8) \\ \\ a=2.45m/s^2 \end{gathered}`

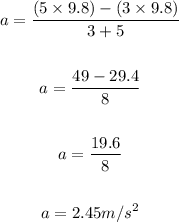
The magnitude of the instantaneous acceleration is 2.45 m/s².

ANSWER:

2.45 m/s²