Let's say the function is :
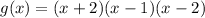
To determine the end behavior, substitute a very large number to x, one for a negative value and one for positive.
So if we substitute a positive large number to x, the sign of the function will be :
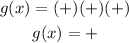
The sign of g(x) will be positive.
And if we substitute a negative large number to x, the sign of the function will be :
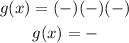
The sign of g(x) will be negative.
So we can conclude that as x goes to + infinity, g(x) goes to + infinity
and as x goes to - infinity, g(x) goes to - infinity
The y-intercept is the value of g(x) when x = 0
Substitute x = 0, then solve for g(x)

Therefore, the y-intercept is at (0, 4)
For the zeros, the zeros are values of x when g(x) = 0
Set g(x) = 0, then solve for x :
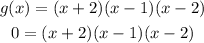
x + 2 = 0 => x = -2
x - 1 = 0 => x = 1
x - 2 = 0 => x = 2
The zeroes are :
(-2, 0), (1, 0) and (2, 0)