We are asked given the following functions:
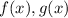
When function are inverses of each other, their composition must be equal to "x", this means:
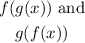
To understand this we need to remember that a function is a rule that assigns an element "x" from one set an element f(x) in another set, as shown in the following diagram:
Therefore, the notation f(x) means that point that is associated with "x" through the function "f". Now, an inverse function takes the value of f(x) and assigns the original "x". We can see this as if the inverse goes in reverse from the original function. This means that if g(x) is inverse of f(x) then g(f(x)) is assigning the original point "x", therefore, the composition of inverse functions will always be "x".
Let's consider the following example. Let's say that we have the following function;
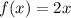
This function assigns to each value of "x" the value "2x". For example, if we substitute x = 2, then the function assigns the value:
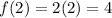
Therefore, for the value x = 2, the function assigns the value f(x) = 4. But now, if we substitute the value x = 1/2, we get:
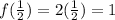
Therefero, for x =1/2, the function assigns the value f(x) = 1.
We could also substitute another function instead of a number, let's say that we substitute the function:
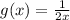
We do the same, but this time we are substituting a function instead of a number:
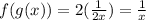
This is called the composition of functions. This means that we substitute a function inside another function. If the substitution of functions is equal to "x", then we say that the functions are inverses of each other. If they are inverses, then the order of composition won't matter and we will get "x". That is, we can substitute g(x) in f(x) or f(x) in g(x) and we would get "x" if they are inverses.