Question

Use the inverse function property to show the given functions are inverses, then explain using asentence why this property shows that that functions are inverses.

Answer 1

Given function :

`f(x)=4x-2`
`g(x)=(x+2)/(4)`

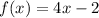
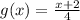
For check the g(x) is a invers of f(x) the any value of x the f(x) output use as g(x) input then value of output of g(x) is equal to "x"

`\begin{gathered} f(x)=4x-2 \\ at\text{ x=2} \\ f(x)=4(2)-2 \\ =8-2 \\ =6 \\ \end{gathered}`

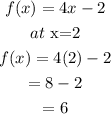
for g(x)

so g(x) is a invers of f(x) .

The property show that convert any function to invers function then value of input convert in output and value of output convert in input that mean x change as y and change as x and above method full fill the condition.