Given function :
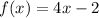
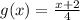
For check the g(x) is a invers of f(x) the any value of x the f(x) output use as g(x) input then value of output of g(x) is equal to "x"
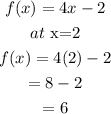
for g(x)
![\begin{gathered} g(x)=(x+2)/(4) \\ \text{the f(x) output is 6 then:} \\ g(6)=(6+2)/(4) \\ =(8)/(4) \\ =2 \end{gathered}]()
so g(x) is a invers of f(x) .
The property show that convert any function to invers function then value of input convert in output and value of output convert in input that mean x change as y and change as x and above method full fill the condition.