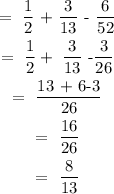Question

=O PROBABILITY AND STATISTICSProbability of selecting one card from a standard deckColorRedRed Diamonds A 2+BlackSpades A4 24Clubs A 24BlackFace cardsJack Queen KingSuit Ace Two Three Four Five Six Seven Eight Nine Ten9♥ 10Hearts A♥ 2♥3♥4♥ 5♥6♥7♥8♥JVQ♥K♥748+9 10 J♦Q+K♦74849410JQK748494 104 JQ+K♣Explanation3434 4434444+ 5+6♦54 6454 64CheckSuppose one card is drawn at random fronAnswer each part. Write your answers as fractions.a standard deck.(a) What is the probability that the card drawn is a red card?0(b) What is the probability that the card drawn is a face card?0(c) What is the probability that the card drawn is a red card or a face card?I need help with this math problem.

Answer 1

1.

The probability that it is a red card.

Total number of red cards (required outcomes)= 26

Total number of cards or sample space = 52

`The\text{ probability that it is a red card = }(26)/(52)\text{ = }(1)/(2)`

2)

Total number of face cards (required outcomes)= 12

Total number of cards or sample space = 52

`Probability\text{ that it is a face card = }(12)/(52)=\text{ }(3)/(13)`

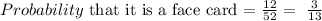
3)

The probability that it is a red or a face card

= probability that it is a red or a face card - probability that it is a red or a face card

`\begin{gathered} =\text{ }(1)/(2)\text{ + }(3)/(13)\text{ - }(6)/(52) \\ =\text{ }(1)/(2)+\text{ }(3)/(13)\text{ -}(3)/(26) \\ =\text{ }\frac{13\text{ + 6-3}}{26} \\ =\text{ }(16)/(26) \\ =\text{ }(8)/(13) \end{gathered}`