We have the progression
91, 85, 79, ..., -29.
Also we can test:
85 - 91 = -6
79 - 85 = - 6
Hence, the progression is an arithmetic progression with d = -6.
Now, using the general formula of an arithmetic progression, we can find the position of term -29; as follows:
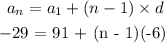
So n = 21
Now we know -29 is the term on the 21 position, we can proceed to find the sum of the first 21st terms of the progression:
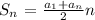
Solving the formula we have:
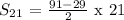
S₂₁ = 651