Answer:
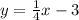
Explanations:
The equation of a line in slope-intercept form is expressed as:

where:
• m is the ,slope
,
• b is the ,y-intercept
From the graph, the y-intercept is the point where the line crosses the y-axis. The y-intercept is (0, -3)
Determine the slope using the coordinate point (0, -3) and (4, -2) on the line
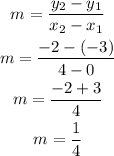
Substitute the slope and y-intercept into the equation to have:
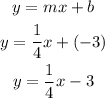
Hence the equation of the line in slope-intercept form is y = 1/4 x - 3