The equation of a line passing through a point A is given as
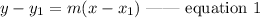
where
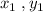
are the coordinates of the point A

In slope-intercept form, we have
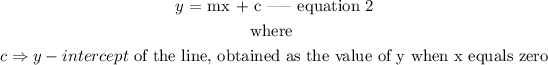
Thus, when
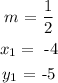
Substitute the above values in equation 1
![\begin{gathered} y\text{ - (-5) = }(1)/(2)(x\text{ - (-4))} \\ y+5\text{ = }(1)/(2)(x+4) \\ \text{open the brackets} \\ y\text{ +5 = }(1)/(2)x\text{ + 2} \\ collect\text{ like terms,} \\ y\text{ = }(1)/(2)x\text{ + 2 -5} \\ \Rightarrow y\text{ = }(1)/(2)x\text{ -3} \\ \end{gathered}]()
Hence, in slope-intercept form, the equation of the line with slope 1/2.and going through the point (-4.-5) is given as

This is in comparison with equation 2, which is the general equation of a line, in slope-intercept form.