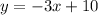Question

Write an equation for the line parallel to the given line that contains C.C(1,7) y = -3x + 4

Answer 1

Recall that the slope intercept equation of a line is of the form y=mx+b where m is the slope and b is the y intercept. In general, two lines are parallel if they look like this

This translates to the fact the the lines never touch each other. This also means that, in a way, the lines increase (or decrease) at the same rate. This notion of rate of increase/decrease is captured by the fact that if we have lines y=m1x+b1 and y=m2x+b2 they are parallel if they have the same slope. That is

`m_1=m_2`

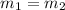
We are given the line y=-3x+4 (with slope -3 and y intercept 4) and we want to find the equation y=mx+b. Since we want that both lines are parallel, based on our previous analysis, we should have

`m=-3`

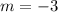
So, so far, our equation looks like this

`y=-3x+b`

Now, we want this line to pass through the point (1,7), this means that whenever x=1, we must have y=7. So, we have the following equation

`7=-3\cdot1+b`

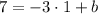
If we add 3 on both sides, we get

`b=7+3=10`

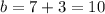
So our final result is the equation

`y=-3x+10`