Question

A card is drawn at random from a standard deck of cards. Find the probability of drawing:

1. A queen or a spade.
II. A black or a face card.
III. A red queen.

Answer 1

Given that a card is drawn at random from a standard deck of cards. We are asked to find the probabilities of

1) A queen or a spade.

2) A black or a face card.

3) A red queen.

This can be seen below;

Step-by-step explanation

The formula for the probability of an event is given as;

`\text{Pr(event) =}\frac{\text{number of events}}{\text{number of total possible outcomes}}`

For a given deck of cards, the number of total possible outcomes is 52 different cards. Next, we find the number of events for each case

`\begin{gathered} n(\text{queen)}=4 \\ n(\text{spades)}=13 \\ n(\text{black)}=26 \\ n(\text{face card)=}12 \\ n(\text{red queen) =2} \end{gathered}`

Therefore we can find the probability in each case. Recall that "or" in probability implies we will add the values of the probabilities we are comparing.

1) A queen or a spade

`Pr(\text{queen or spade)= }(4)/(52)+(13)/(52)=(17)/(52)`

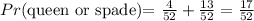
Answer

`Pr(\text{queen or spade)=}(17)/(52)`

2) A black or a face card

`Pr(black\text{ or }facecard)=(26)/(52)+(12)/(52)=(38)/(52)=(19)/(26)`

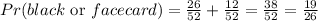
Answer:

`Pr(\text{black or facecard)=}\frac{\text{19}}{26}`

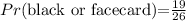
3) A red queen

`Pr(A\text{ }red\text{ }queen)=(2)/(52)=(1)/(26)`

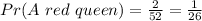
Answer

`Pr(A\text{ }red\text{ }queen)=(1)/(26)`