Answer:
(a)3,003 ways.
(b)360,360 ways.
Step-by-step explanation:
• The number of colors = 15
,
• The number of colors to be chosen = 5
(a)If the order of choices is not relevant we use the combination formula:
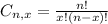
In this problem: n=15, x=5
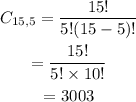
This can be done in 3,003 ways.
(b)If the order of choices is relevant we use the permutation formula:
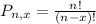
In this problem: n=15, x=5
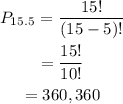
This can be done in 360,360 ways.