We know that
• The plane travels 1440 miles in 3 hours with the wind.
,
• It takes 4 hours against the wind to travel the same distance.
Let's call p the rate of the plane in still air, and w the speed of the wind.
Traveling with the wind would be expressed as follows.
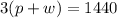
This expression is deducted from the distance formula d = v*t.
The expression that represents against the wind would be.
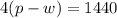
To solve the system we just formed.
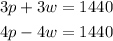
Let's multiply the first equation by 4 and the second equation by 3.
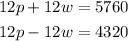
Now, let's combine the equations.
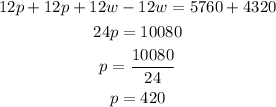
The rate of the plane in still air is 420 miles per hour.
Now, let's find w.
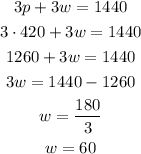
The rate of the wind is 60 miles per hour.