Question

When a plane flies with the wind, it can travel 1440 miles in 3 hours. When the plane flies in the opposite direction against the wind it takes 4 hours to fly the same distance. Find the rate of the plane in still air Find the rate of the wind

Answer 1

We know that

• The plane travels 1440 miles in 3 hours with the wind.

,

• It takes 4 hours against the wind to travel the same distance.

Let's call p the rate of the plane in still air, and w the speed of the wind.

Traveling with the wind would be expressed as follows.

`3(p+w)=1440`

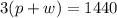
This expression is deducted from the distance formula d = v*t.

The expression that represents against the wind would be.

`4(p-w)=1440`

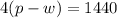
To solve the system we just formed.

`\begin{gathered} 3p+3w=1440 \\ 4p-4w=1440 \end{gathered}`

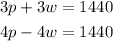
Let's multiply the first equation by 4 and the second equation by 3.

`\begin{gathered} 12p+12w=5760 \\ 12p-12w=4320 \end{gathered}`

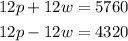
Now, let's combine the equations.

`\begin{gathered} 12p+12p+12w-12w=5760+4320 \\ 24p=10080 \\ p=(10080)/(24) \\ p=420 \end{gathered}`

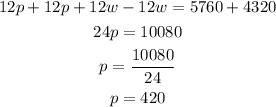
The rate of the plane in still air is 420 miles per hour.

Now, let's find w.

`\begin{gathered} 3p+3w=1440 \\ 3\cdot420+3w=1440 \\ 1260+3w=1440 \\ 3w=1440-1260 \\ w=(180)/(3) \\ w=60 \end{gathered}`

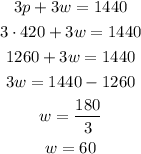
The rate of the wind is 60 miles per hour.