Answer:
D. 72.6 mm²
Step-by-step explanation:
The area of the triangle can be calculated by Heron's Formula:
![A=\sqrt[]{s(s-a)(s-b)(s-c)}](https://img.qammunity.org/2023/formulas/mathematics/college/t3rmhsk71nltcmgtu237bvtgrmrx89v4xv.png)
Where a, b, and c, are the legs and s can be calculated as:
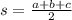
Therefore, replacing a, b, and c by 15, 10, and 20, we get that s is equal to:

Then, the area of the triangle will be equal to:
![\begin{gathered} A=\sqrt[]{22.5(22.5-15)(22.5-10)(22.5-20)} \\ A=\sqrt[]{22.5(7.5)(12.5)(2.5)} \\ A=\sqrt[]{5273.44} \\ A=72.6mm^2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/g6uuvmx9xvv2jqqakccsoz37xg7a1y1hkj.png)
So, the answer is:
D. 72.6 mm²