Question

At what rate is his distance increasing from home plate when he is 20 feet from second base

Answer 1

Let's take a look at our situation:

Notice that we can construct a right triangle from this situation!

The key concept here is that the distance bewteen the runner and second base will be a function of x. More specifically, 21x.

Now, we use the Pythagorean Theorem, to conclude that:

`d^2=90^2+\mleft(21x\mright)^2`

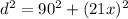
If we solve for d, we would have a function for the distance between the runner and home plate in terms of x :

`\begin{gathered} d=\sqrt[]{90^2+\mleft(21x\mright)^2} \\ \\ \Rightarrow d(x)=\sqrt[]{8100+441x^2} \end{gathered}`

Now, to calculate the rate of change for this function, we calculate the derivative. Using the chain rule and simplifying, we can conclude that:

`d^(\prime)(x)=\frac{147}{\sqrt[]{49x+900}}`

Now, we're being asked for the instant of time where the runner is 20 feet from second base. The time when this happens is:

`\begin{gathered} 21x=20 \\ \\ \Rightarrow x=(20)/(21) \end{gathered}`

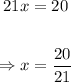
Now, let's evaluate the derivative for this value of x:

`\begin{gathered} d^(\prime)((20)/(21))=\frac{147}{\sqrt[]{49((20)/(21))+900}} \\ \\ \Rightarrow4.78\text{ ft per second} \end{gathered}`

Therefore, the rate at which the distance from the runner to home plate increases when he's 20 feet from second base is 4.78 feet per second.