Let's take a look at our situation:
Notice that we can construct a right triangle from this situation!
The key concept here is that the distance bewteen the runner and second base will be a function of x. More specifically, 21x.
Now, we use the Pythagorean Theorem, to conclude that:
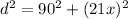
If we solve for d, we would have a function for the distance between the runner and home plate in terms of x :
![\begin{gathered} d=\sqrt[]{90^2+\mleft(21x\mright)^2} \\ \\ \Rightarrow d(x)=\sqrt[]{8100+441x^2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/izf2cvm46a7jy3onmjr3yijhgnyz0v0nek.png)
Now, to calculate the rate of change for this function, we calculate the derivative. Using the chain rule and simplifying, we can conclude that:
![d^(\prime)(x)=\frac{147}{\sqrt[]{49x+900}}](https://img.qammunity.org/2023/formulas/mathematics/college/gtbpnmzhvqvlq4mir8ah8kyz0oytg7i4rf.png)
Now, we're being asked for the instant of time where the runner is 20 feet from second base. The time when this happens is:

Now, let's evaluate the derivative for this value of x:
![\begin{gathered} d^(\prime)((20)/(21))=\frac{147}{\sqrt[]{49((20)/(21))+900}} \\ \\ \Rightarrow4.78\text{ ft per second} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/iijfd8j8e4wjhc7ets3pi42743zmrumvyd.png)
Therefore, the rate at which the distance from the runner to home plate increases when he's 20 feet from second base is 4.78 feet per second.