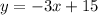Answer:
The equation of a line perpendicular to the given line and passes through the given point is:
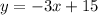
Step-by-step explanation:
Given the line:
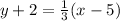
This can be rewritten as:
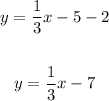
This is a line with slope 1/3, and y-intercept -7.
A line perpendicular to this line has it's slope as the negative reciprocal of 1/3.
The negativen reciprocal of 1/3 is -3.
So, the line is of the form:

We can find the y-intercept b, by using the given point, (4, 3) in the perpendicular equation we formend.
Where x = 4, and y = 3
Doing this, we have:

Add 12 to both sides
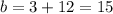
Therefore, the equation of a line perpendicular to the given line and passes through the given point is: