Question

A solution is made byequilibrating the twosolids calcium sulfide(Ksp = 8.0x10-6) andcalcium carbonate (Ksp3.8x10-9) with water.=What are theconcentrations of thethree ions at equilibrium,if some of each of thesolids remain?[Ca2+] =[S²] =[CO3²-] =MMM

Answer 1

Given data:

CaS Ksp = 8.0x10^-6

CaCO3 Ksp = 3.8x10^-9

Let's start by writing down the chemical equation that refers to each solubility constant.

`\begin{gathered} CaS\rightleftarrows Ca^(2+)+S^(2-)\text{ Ksp = }8.0*10^(-6) \\ \\ CaCO_3\rightleftarrows Ca^(2+)+CO_3^-\text{ Ksp = }3.8*10^(-9) \end{gathered}`

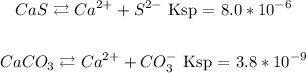
Now let's first discover the concentration of Ca from the solubility of CaS.

`Ksp=[Ca^(2+)][S^(2-)]`

Since the stoichiometric relation of the two ions in this reaction is 1:1, we can assume the same concentration in mol/L. Let's call this same concentration as letter S for now.

Ksp = S * S

Ksp = S^2

8.0x10^-6 = S^2

`\begin{gathered} S=\sqrt{8.0*10^(-6)} \\ \\ S=0.0023\text{ mol/L} \end{gathered}`

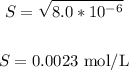
This is the concentration of Ca2+ from CaS.

Now doing the same for CaCO3:

`CaCO_3\rightleftarrows Ca^(2+)+CO_3^-`
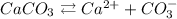
`\begin{gathered} Ksp\text{ = \lbrack Ca}^(2+)][CO_3^-] \\ Ksp\text{ = S*S} \\ Ksp=S^2 \\ 3.8*10^(-9)=S^2 \\ S=\sqrt{3.8*10^(-9)} \\ S=6.2*10^(-5)\text{ mol/L} \end{gathered}`

This is the concentration of Ca2+ from CaCO3.

So we have the following final relation of concentrations:

[Ca2+] = 0.0023 + 6.2*10^-5

[Ca2+] = 0.00236 M

[S2-] = 0.00230 M

[CO3 2-] = 6.2*10^-5 M

[Ca2+] = 2.36*10^-3 M

[S2-] = 2.30*10^-3 M

[CO3 2-] = 6.2*10^-5 M

[Ca2+] = 0.00236 M

[S2-] = 0.00230 M

[CO3 2-] = 0.00006.2 M