To get the mean of a set of data, the steps are to add all the data and divide by the total number of data.
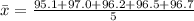
Then, solve.
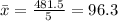
The mean is 96.3 grams.
On the other hand, the median of a set of data is the middlemost data once the data has been arranged from lowest to highest or vice versa.
Let's arrange the data first.
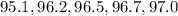
Out of the 5 data, the middlemost data would be the third one. Hence, the median is 96.5 grams.