The volume of a pyramid is one third of the product between the base area and the height:
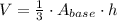
We already know the height of the pyramid, however we need to estimate the base area from the information given.
The base is a square. Squares have their four sides with the exat same length.
The perimeter is the sum of the length of the sides of a polygon, then, the perimeter of the square is four times its side:

Where L is the length of the side. Now, knowing the perimeter we can estimate the lenght of the sides of the base, from which we can calculate the base area:
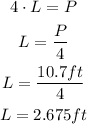
Now we know the sides of the base have a length of 2.675 ft each. To estimate the area of the base we just need to square this lenght:
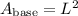
Then, to calculate the volume of the pyramid:

Let's replace values:

The volume of the pyramid is approximately 23.4 cubic feet.