Part A:
In 2000, the population was 6.26 million.
In 2015, the population was 7 million.
The general form of the exponential function is given by
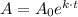
Where A0 is the initial population (6.26 million), k is the growth rate, and t is the number of years after 2000.
Let us first find the growth rate.
We are given that In 2015, the population was 7 million.
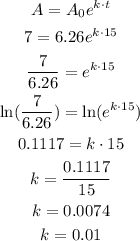
So, the growth rate is 0.01 (rounded to 2 decimal places)
Therefore, the exponential growth model is
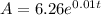
Part B:
We need to find the year for which the population will be 12 million.
Let us substitute A = 12 into the exponential growth function and solve for t
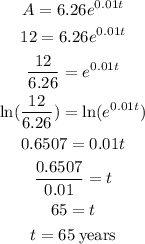
Therefore, the country's population will be 12 million in the year 2065