For the shape ABCD to be a parallelogram, the sides AB and CD must be parallel:
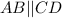
Hence, line BD is the transversal.
Note that angles ABD and CDB are alternate interior angles. By definition, the angles will be equal:
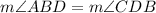
Therefore, substituting the values of the angles will yield the following equation:
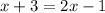
Solving the equation for x:
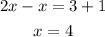
Therefore, the correct option is the THIRD OPTION.