Question

A) Given the below function in vertex form, determine what the vertex and axis of symmetry would be when you graph the function. You are not required to graph the function. F(x) = 2(x+3)^2-6 B) Now write the above function in standard form and use it to identify the y-intercept.

Answer 1

Given:

The equation is,

`F(x)=2(x+3)^2-6\ldots\ldots\ldots\ldots(1)`

A) Compare given equation with vertex form of quadratic equation,

`\begin{gathered} F(x)=a(x-h)^2+k \\ (h,k)=\text{ vertex} \\ x=h\text{ is the axis of symmetry} \end{gathered}`

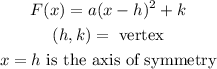
It implies that,

`\begin{gathered} F(x)=2(x+3)^2-6 \\ F(x)=2(x-(-3))^2+(-6) \\ \text{vertex}=(h,k)=(-3,-6) \\ \text{Axis of symmetry is x=-3} \end{gathered}`

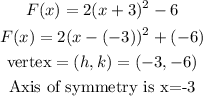
B) To identify the y- intercept,

Put x=0 in equation (1)

`\begin{gathered} F(x)=2(x+3)^2-6 \\ F(0)=2(0+3)^2-6 \\ \Rightarrow18-6=12 \end{gathered}`

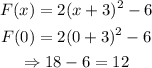
Y- intercept is at y=12.

Answer:

A) Vertex= (-3,-6) and axis of symmetry x=-3.

B) y-intercept y=12.