Question

17.) The base of a triangle is 1 meter more than three times the height.Set up and solve an equation to find the base and the height if the1area is 40 square meters. Use: z(base)(height) = Area(12 pts)

Answer 1

Step 1: List out the given parameters.

`\begin{gathered} \text{Let the height be x} \\ \text{Base}=3x+1 \\ A=40m^2 \end{gathered}`

Step 2: Write the formula for the area of the triangle and solve.

`\begin{gathered} A=(1)/(2)*\text{base x height} \\ \end{gathered}`

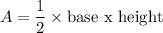
Substitute the parameters in step 1 into the formula in step 2

`\begin{gathered} 40=(1)/(2)*(3x+1)* x \\ 80=3x^2+x \\ 3x^2+x-80=0 \end{gathered}`

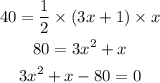
Solving the above quadratic equation by quadratic formula method, we will get:

`x=5\text{ and x=}(-16)/(3)`

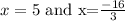
Since the value for a side of a triangle cannot be negative, x=5 is the only value of x we can use.

Therefore:

`\begin{gathered} \text{height}=x=5m \\ \text{Base}=(3x+1)=(3(5)+1)=(15+1)=16m \end{gathered}`

So we can conclude that:

The base is 16 meters and the height is 5 meters.