SOLUTION
Step 1: List out the given parameters.
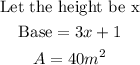
Step 2: Write the formula for the area of the triangle and solve.
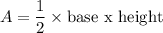
Substitute the parameters in step 1 into the formula in step 2
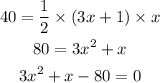
Solving the above quadratic equation by quadratic formula method, we will get:
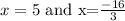
Since the value for a side of a triangle cannot be negative, x=5 is the only value of x we can use.
Therefore:
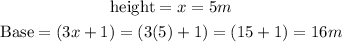
So we can conclude that:
The base is 16 meters and the height is 5 meters.