perpendicularWe were given the following information:
The equation of a line is given by: y = - 1/4 x + 9
We want to obtain the equation for a line perpendicular to this line & that passes through the point (4, -8). This is shown below:
The general equation of a straight line is given by:
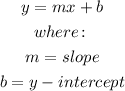
The equation of the line given us is:

The relationship between the slope of a line and the slope of a line perpendicular to it is given by the statement "the product of the slopes of two lines perpendicular to one another is negative one"
This is expressed below:

Therefore, the slope of the perpendicular line is: 4
We were told that the perpendicular line passes through the point (4, -8). We will obtain the equation of the perpendicular line using the Point-Slope equation. This is shown below:

The graphical representation of this is given below: