Question

Two similar pyramids have slant heights of 4 and 6.1) Find the scale factor.2) If the volume of the smaller pyramid is 48 meters cubed, what is the volume of the larger pyramid?

Answer 1

`\begin{gathered} 1)(3)/(2)\text{ or 1.5} \\ 2)162m^3 \end{gathered}`

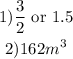
Step-by-step explanation

1) The slant heights of the pyramids are 4 and 6.

The scale factor is the ratio of the corresponding sides of two figures, hence, the scale factor of the two pyramids is:

`\begin{gathered} (6)/(4) \\ \Rightarrow(3)/(2)\text{ or 1.5} \end{gathered}`

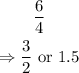
2) The ratio of the volumes of two similar figures is equal to the cube of their scale factor.

Let the volume of the bigger pyramid be p.

This means that:

`\begin{gathered} (p)/(48)=((3)/(2))^3 \\ \Rightarrow(p)/(48)=(27)/(8) \end{gathered}`

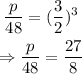
Solve for p by cross-multiplying:

`\begin{gathered} p=(27\cdot48)/(8) \\ p=162m^3 \end{gathered}`

That is the volume of the larger pyramid.