ANSWER
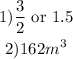
Step-by-step explanation
1) The slant heights of the pyramids are 4 and 6.
The scale factor is the ratio of the corresponding sides of two figures, hence, the scale factor of the two pyramids is:
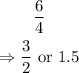
2) The ratio of the volumes of two similar figures is equal to the cube of their scale factor.
Let the volume of the bigger pyramid be p.
This means that:
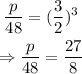
Solve for p by cross-multiplying:
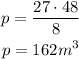
That is the volume of the larger pyramid.