We will answer the question a) using the following formula:

where we have the following event:

Therefore, the probability P(N|T) is the probability of a randomly selected adult use non-prescription antidepressants given that he visited the therapist. This formula is known as conditional probability formula.
To use the formula, we have to calculate the probability :
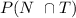
This is the probability of the intersection between the events N and T, that is, the probability that a given adult visits a therapist and use non-prescription antidepressants. Thsi information was given in the question, so we have

Therefore, we can calculate the probability required in the part a) as :
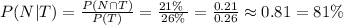
Therefore, the answer for the part a) is 81%, or in decimal number 0.81.
Part b)
We are asked to calculate the probability of that a randomly selected patient who use non-prescription antidepressants visit the therapist. This can be written in symbols as (we use the notations from the solution of the part a))
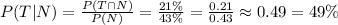
Therefore, the answer for the part b) is 49%, or in decimal number 0.49.