To solve the exercise, replace the coordinates of the points into the given equation.
If after operating, the result is a true proposition then the point belongs to the graph of the equation.
If after operating, the result is a false statement then the point does not belong to the graph of the equation.
Point (A) (-3,6)

Therefore, the point is not on the graph of the equation.
Point (B) (-2,0)

Therefore, the point is not on the graph of the equation.
Point (C) (0,-2)
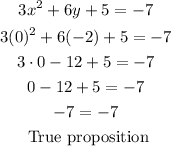
Therefore, the point is on the graph of the equation.
Point (D) (8,2)

Therefore, the point is not on the graph of the equation.
Finally, the only point that is on the graph of the equation is point C.
Graphically