We are asked to determine a linear model that relates the time and height of a person.
Let "x" be the time since birth and "y" the height, then we are given the following points:
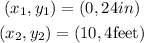
Now, we convert the inches to feet using the following conversion factor:
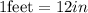
Now, we multiply by the conversion factor:
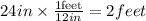
Therefore, the points are:
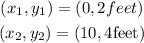
Now, we determine the slope of the line using the following formula:
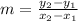
Substituting the values we get:
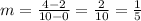
Now, we use the general form of a line equation in slope-intercept form:
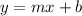
Where "m" is the slope and "b" is the y-intercept. Now, we substitute the value of the slope:
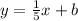
To determine the value of "b" we will substitute the first point:
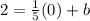
Solving the operations:
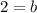
Therefore, the value of "b" is 2:
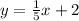
Now, we substitute the value "x= 9", we get:
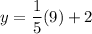
Solving the operations:
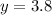
Therefore, the height at age 9 is 3.8 feet.