Question

Suppose that you were 24 inches long at birth and 4 feet tall on your tenth birthday. Based on these two datapoints, create a linear equation for the function that describes how height varies with age. Use the equationto predict the height at age 9.

Answer 1

We are asked to determine a linear model that relates the time and height of a person.

Let "x" be the time since birth and "y" the height, then we are given the following points:

`\begin{gathered} (x_1,y_1)=(0,24in) \\ (x_2,y_2)=(10,4\text{feet)} \end{gathered}`

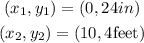
Now, we convert the inches to feet using the following conversion factor:

`1\text{feet}=12in`

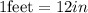
Now, we multiply by the conversion factor:

`24in*\frac{1\text{feet}}{12in}=2feet`

Therefore, the points are:

`\begin{gathered} (x_1,y_1)=(0,2feet) \\ (x_2,y_2)=(10,4\text{feet)} \end{gathered}`

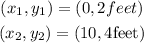
Now, we determine the slope of the line using the following formula:

`m=(y_2-y_1)/(x_2-x_1)`

Substituting the values we get:

`m=(4-2)/(10-0)=(2)/(10)=(1)/(5)`

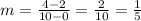
Now, we use the general form of a line equation in slope-intercept form:

`y=mx+b`

Where "m" is the slope and "b" is the y-intercept. Now, we substitute the value of the slope:

`y=(1)/(5)x+b`

To determine the value of "b" we will substitute the first point:

`2=(1)/(5)(0)+b`

Solving the operations:

`2=b`

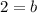
Therefore, the value of "b" is 2:

`y=(1)/(5)x+2`

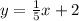
Now, we substitute the value "x= 9", we get:

`\begin{gathered} y=(1)/(5)(9)+2 \\ \end{gathered}`

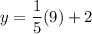
Solving the operations:

`y=3.8`

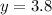
Therefore, the height at age 9 is 3.8 feet.