ANSWER:
444 N
Explanation:
We can calculate the force, by means of Pascal's principle, which is stated as follows
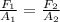
We need to know F1, which would be the force exerted on the small input piston, we solve for F1:

The input force is exerted on the small input piston is 444 N