Question

There is part 2 but it won't let me post until part 1 is done

Answer 1

Given the function:

`k(x)=(x^3-8x-32)/(x-4)`

We need to find the value of k(x) when x = 3.9 and x = 3.999 and x = 4.001

So, for each value of x we will substitute into the function k(x)

when x = 3.9

`k(x)=(3.9^3-8\cdot3.9-32)/(3.9-4)=(-3.881)/(-0.1)=38.81`

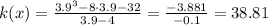
When x = 3.999

`k(x)=(3.999^3-8\cdot3.999-32)/(3.999-4)=(-0.039988)/(-0.001)=39.9880012`

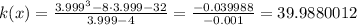
When x = 4.001

`k(x)=(4.001^3-8\cdot4.001-32)/(4.001-4)=(0.040012)/(0.001)=40.0120007`

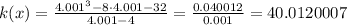
When x = 4.1

`k(x)=(4.1^3-8\cdot4.1-32)/(4.1-4)=(4.121)/(0.1)=41.21`

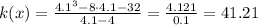
So, we can deduce that The limit of the function = 40