Given the function:
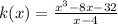
We need to find the value of k(x) when x = 3.9 and x = 3.999 and x = 4.001
So, for each value of x we will substitute into the function k(x)
when x = 3.9
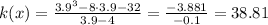
When x = 3.999
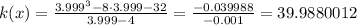
When x = 4.001
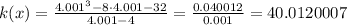
When x = 4.1
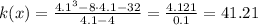
So, we can deduce that The limit of the function = 40