The directrix of the parabola is a vertical line at x = -4 and the focus is at the right of the directrix at (1, 3). This means the parabola is horizontal and it opens to the right.
The equation of a vertical parabola is:
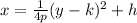
Where (h, k) are the vertex coordinates, and the vertex is at the midpoint between the focus and the directrix.
The y-coordinate of the vertex is k = 3 and the x-coordinate is:
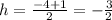
p is the distance from the vertex to the focus:
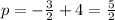
Thus:
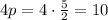
Now we can substitute all the values into the equation:
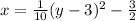
This is the required vertex form of the parabola.