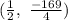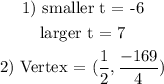
1) To get the zeros of the function, we have to equate the function to zero and solve for the roots of the quadratic equation
We have this as follows;

smaller t is -6
Larger t is 7
2) We want to get the vertex of the parabola
To get this, we need to write thw function in the vertex form
We have the vertex form as;

The vertex of the parabola is the point (h,k)
We can write the vertex form as follows;
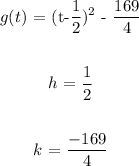
The vertex of the parabola is thus;