Question

Hello So a lot of people said that they cannot help me and it is not in their expertise but hopefully whoever gets me this time can because I really need it. I posted a picture but basically there are graphs and tables and we are supposed to describe the rate of change and then explain our reasoning. Help with question D and not E because I know you are only meant to do one question per session.

Answer 1

Sequence D:

If we have to graph the sequence, we should do:F

We derive the graph and the table from the sequence.

The sequence final step is two dots because it seems that the number of dots increase by two in each step until step 3 and then start to descend by 2. Then, if step 4 is 4 dots, then step 5 is 2 dots.

The overall rate of change is 0, as if we compare the last and intial state, we have the same value.

Sequence E:

We have to complete the sequence. We can think that each step a new line is added at the left side and at the botton.

We are increasing with the formula:

`n^2+1`

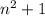
where n is the step number.

We can think of a square with side n and and additional dot.

Then, the fifth step is:

NOTE: The table is correct, as the fifth value is 5^2+1 = 25 +1 = 26.

The graph will be:

The sequence logic is the square of the number of step n plus one dot.

Then, its average rate of change between the initial state and the final state can be written as:

`(f(5)-f(1))/(5-1)=(26-1)/(5-1)=(25)/(4)\approx6.25`

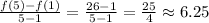
The rate of change is not constant: it is increasing with the number of steps.