Question

Find the values of both variables. answers must be in variable form.

Answer 1

ANSWERS

• x = 6√3

,

• y = 12

Step-by-step explanation

This is a right triangle. We know the measure of one of the angles, and the length of the leg adjacent to this angle. We have to find the length of the opposite leg and the length of the hypotenuse. To find these, we will use trigonometric ratios,

`\tan 60\text{\degree}=(x)/(6)`

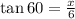
Multiply both sides by 6 to solve for x,

`x=6\tan 60\text{\degree}=6\cdot\sqrt[]{3}`

For x we will use the cosine,

`\cos 60\text{\degree}=(6)/(y)`

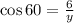
Solve for y,

`y=\frac{6}{cos60\text{\degree}}=(6)/((1)/(2))=12`

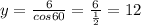
Hence, x = 6√3 and y = 12.