Question

Michelle has money in two savings accounts. One rate is 6% and the other is 14 %. If she has $900 more in the 14 % account and the total interest is $209. how muchis invested in each savings account?

Answer 1

The Solution:

Let the amount in the savings account with 6% interest rate be represented with $x

So, the interest in this account is given as below:

`\begin{gathered} I_1=\frac{\text{PRT}}{100}=(x*6*1)/(100)=(6x)/(100) \\ \text{where} \\ I_1=\text{interest}=\text{?,P}=\text{amount saved=x, T=time=1 (assumed)} \end{gathered}`

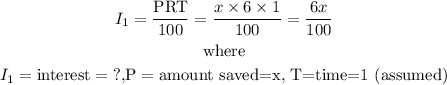
Similarly, the amount in the savings account with 14% interest rate will be $(x+900)

So, the interest in this account is given as below:

`\begin{gathered} I_2=\frac{\text{PRT}}{100}=((x+900)*14*1)/(100)=(14x+12600)/(100) \\ \text{where} \\ I_2=\text{interest}=\text{?,P}=\text{amount saved=x+900, T=time=1 (assumed)} \end{gathered}`

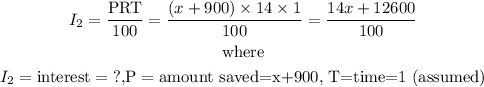
So, the total interest from the two savings accounts is $209. That is,

`I_1+I_2=(6x)/(100)+(14x+12600)/(100)=209`

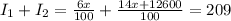
This becomes

`\begin{gathered} (6x+14x+12600)/(100)=209 \\ \\ (20x+12600)/(100)=209 \end{gathered}`

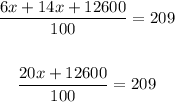
Cross multiplying, we get

`\begin{gathered} 20x+12600=100*209 \\ 20x+12600=20900 \end{gathered}`

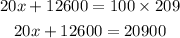
Collecting the like terms, we get

`\begin{gathered} 20x=20900-12600 \\ 20x=8300 \end{gathered}`

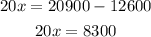
Dividing both sides by 20, we get

`\begin{gathered} (20x)/(20)=(8300)/(20) \\ \\ x=\text{ \$415} \end{gathered}`

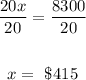
So, the amount invested in the savings account that yields 6% is $415.00, while

the amount invested in the savings account that yields 14% is $1315.00 ( that is, 415+900)