Question

A ship leaves Port A and travels 66 miles due west to point C. If then adjusts to course 34° northward. It travels 80 miles in that direction until it reaches Port B. What angle 0 with respect to sue north could the ship have used to travel directly from Port A to Port B? See the figure below.

Answer 1

The figure shows the geometric construction related to the problem.

We need to complete the figure with some extra variables.

The triangle with sides of 80 miles, x, and y is a right triangle. We can apply trigonometric ratios. For example, the sine of 34° is the ratio of the opposite side (y) and the hypotenuse (80), thus:

`sin34\degree=(y)/(80)`

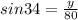
Solving for y:

`y=80sin34\degree`

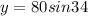
We'll leave the calculations for later. Now apply the cosine ratio:

`cos34\degree=(x)/(80)`

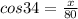
Or, equivalently:

`x=80cos34\degree`

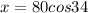
Now focus on the upper triangle (another right triangle) with legs of length x + 66 and y. We can apply the tangent of the unknown angle to find its measure as follows:

`tan\theta=(x+66)/(y)`

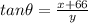
Recall the tangent ratio is the ratio between the opposite leg and the adjacent leg.

Substituting the determined values of x and y:

`tan\theta=(80cos34\degree+66)/(80sin34\degree)`

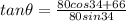
Calculating (we need a scientific calculator):

`\begin{gathered} tan\theta=(66.3230+66)/(44.7354) \\ \\ tan\theta=2.9579 \end{gathered}`

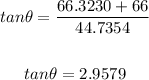
Now calculate the value of the angle with the inverse tangent function:

`\begin{gathered} \theta=arctan(2.9579) \\ \\ \theta=71.3\degree \end{gathered}`

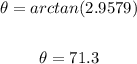
Answer: 71.3°