The figure shows the geometric construction related to the problem.
We need to complete the figure with some extra variables.
The triangle with sides of 80 miles, x, and y is a right triangle. We can apply trigonometric ratios. For example, the sine of 34° is the ratio of the opposite side (y) and the hypotenuse (80), thus:

Solving for y:
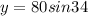
We'll leave the calculations for later. Now apply the cosine ratio:

Or, equivalently:
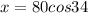
Now focus on the upper triangle (another right triangle) with legs of length x + 66 and y. We can apply the tangent of the unknown angle to find its measure as follows:
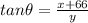
Recall the tangent ratio is the ratio between the opposite leg and the adjacent leg.
Substituting the determined values of x and y:
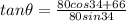
Calculating (we need a scientific calculator):
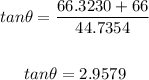
Now calculate the value of the angle with the inverse tangent function:

Answer: 71.3°