We need to use the formal definition of a limit, The definition is:
Let be L be a real number. Then:
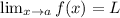
if, for every ε > 0, there exists a δ > 0 such that if 0 < |x - a| < δ, then |f(x) - L| < ε
In this case, we need to prove:
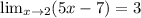
Then, we need to find a relationship between ε and δ, so for any value of ε> 0 we can find a value of δ.
We know that, for a given ε > 0, |(5x -7) - 3| < ε, and 0 < |x - 2| < δ
Then:
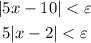
Now we can divide each side by 5.
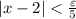
We are now really close from relate the ε and δ.
We can use the triangle inequality:
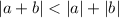
Then, we can add and subtract 1 inside the absolute value:
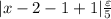
We have:
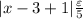
By the triangle inequality:
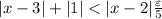
And since the absolute value of any number is bigger or equal than 0:
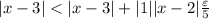
And we have:
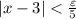
And since ε > 0, ε/5 > 0, we can define:
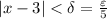
And we have proven that:
For a given ε > 0, exists δ = ε/5 such that, if 0 < |x - 2| < δ = ε/5, then |f(x) - L| < ε