hello
the points given are (-4, 47) and (2, -16)
let's find the intercept of this equation
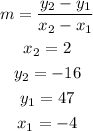
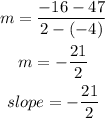
now, since we know the value of the slope, we can use that in the standard equation on a straight line
the standard equation of a straight line is given as
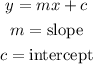
we can pick any of the points and solve for intercept
let's use (2, -16)
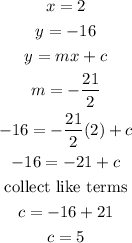
now we know the value of intercept (c) = 5 and the slope (m) = 21/2
let's use this to write equation of the straight line
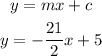
from the calculations above, the equation of the straight line is given as y = -21/2x + 5