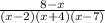Question

Help I don’t understand For the first one you just have to locate and describe the error made by the student was subtracting the rational expressionAnd the second one is to fix the students error and correctly subtract the rational function

Answer 1

Given:

`(x+2)/(x^2-3x-28)-(x-3)/(x^2-9x+14)`

Required:

We need to subtract the given fractions.

Step-by-step explanation:

A)

Factoring the denominators:

`(x+2)/(x^2-7x+4x-28)-(x-3)/(x^2-7x-2x+14)`

`(x+2)/(x(x-7)+4(x-7))-(x-3)/(x(x-7)-2(x-7))`

`(x+2)/((x-7)(x+4))-(x-3)/((x-7)(x-2))`

`(x+2)/((x+4)\left(x-7\right))-(x-3)/((x-2)\left(x-7\right))`

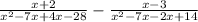
Generating LCD:

`(x+4)(x-7)(x-2)`

Renaming:

`(x-2)/(x-2)*(x+2)/((x+4)\left(x-7\right))-(x-3)/((x-2)\left(x-7\right))*(x+4)/(x+4)`

Simplifying:

`((x+2)(x-2))/((x-2)(x+4)\left(x-7\right))-((x-3)(x+4))/((x-2)(x+4)\left(x-7\right))`

`((x^2-2^2))/((x-2)(x+4)\left(x-7\right))-(x\left(x+4\right)-3\left(x+4\right))/((x-2)(x+4)\left(x-7\right))`

`((x^2-4))/((x-2)(x+4)\left(x-7\right))-(x^2+4x-3x-12)/((x-2)(x+4)\left(x-7\right))`

`((x^2-4))/((x-2)(x+4)\left(x-7\right))-(x^2+x-12)/((x-2)(x+4)\left(x-7\right))`

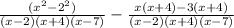
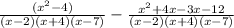
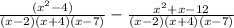
Distributing the minus sign.

`(x^2-4-x^2-x-(-12))/((x-2)(x+4)\left(x-7\right))`

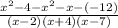
The student made an error in distributing the minus sign.

The student used x instead of -x in the numerator.

The sign of x should be negative.

The student used -12 instead of +12 in the numerator.

B)

The correct form of distributing the minus sign.

`(x^2-4-x^2-x+12)/((x-2)(x+4)\left(x-7\right))`

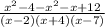
Final answer:

`(8-x)/((x-2)(x+4)\left(x-7\right))`