Question

Can the equation x^2 - 8x + 18 = 0 be solved by factoring? X=

Answer 1

Given the equation:

`x^2-8x+18=0`

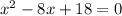
a = 1, b = -8, c = 18

We will calculate the discriminant D

`D=b^2-4ac`

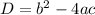
Substitute with a, b, and c

`D=(-8)^2-4\cdot1\cdot18=-8`

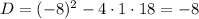
As the value of (D) is negative the solution to the equation can't be solved by factoring

There are two complex values for x

`x=\frac{-b\pm\sqrt[]{D}}{2a}`

Substitute with a, b, and D

So, the values of x will be:

`x=\frac{8\pm\sqrt[]{-8}}{2\cdot1}=\frac{8\pm i2\sqrt[]{2}}{2}=4\pm i\sqrt[]{2}`

so, the answer will be:

`x=4\pm i\sqrt[]{2}`