Given the equation:
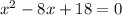
a = 1, b = -8, c = 18
We will calculate the discriminant D
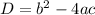
Substitute with a, b, and c
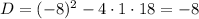
As the value of (D) is negative the solution to the equation can't be solved by factoring
There are two complex values for x
![x=\frac{-b\pm\sqrt[]{D}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/yk6b94ddmrrpyxtidl1xyxx873xcmmceih.png)
Substitute with a, b, and D
So, the values of x will be:
![x=\frac{8\pm\sqrt[]{-8}}{2\cdot1}=\frac{8\pm i2\sqrt[]{2}}{2}=4\pm i\sqrt[]{2}](https://img.qammunity.org/2023/formulas/mathematics/college/8cvf046net2ittxjd9nhby5dtp9focxinq.png)
so, the answer will be:
![x=4\pm i\sqrt[]{2}](https://img.qammunity.org/2023/formulas/mathematics/college/q3yf3oxazdlffkcgzd0wnaur0wz8gxfrlk.png)