Question

Triangle XYZ is pictured below. Line WY is a perpendicular bisector to side XZ. What is thevalue of x?12x5W129N

Answer 1

We are given a triangle and told that line WY is a perpendicular bisector to side XZ. This line basically splits the triangle into two triangles: XYW and YZW.

Note that as both triangles have two pairs of sides with the same length and a congruent angle (angles XWY and YWZ are both 90°), both triangles are congruent. THat is, corresponding sides have the same length.

This leads to having sides XY and YZ to be congruent. So we have the equation

`12x\text{ -5=129}`

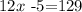
first, we add 5 on both sides. So we get

`12x=129+5=134`

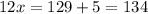
Finally, we divide both sides by 12. We get

`x=(134)/(12)`

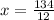
Note that

`x=(132+2)/(12)=(132)/(12)+(2)/(12)=11+(1)/(6)`

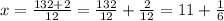
so we have that

`x=11(1)/(6)`